Задачи заочного тура олимпиады по математике

7.1.
Является ли число 1 + 2000^19991998 простым?

7.2.
Имеется 6 одинаковых по виду монет, из которых 4 настоящие, весом 4 грамма каждая, а 2 -- фальшивые, отличающиеся от настоящих по весу. Фальшивые монеты в сумме весят 8 граммов. Также имеются чашечные весы (без гирь). Как определить обе фальшивые монеты за 4 взвешивания?

7.3.
Числа a, b, c и d -- целые, удовлетворяющие условию a + b + c + d = 0. Докажите, что число a² + b² + c² + d² может быть представлено как сумма квадратов трех некоторых натуральных чисел.

7.4.
Диагонали четырехугольника пересекаются внутри этого четырехугольника. Обозначим через S сумму длин его диагоналей, через P -- периметр. Докажите, что справедливо двойное неравенство S < P < 2S.

8.1.
Шестизначное число делится на 37. Его первая и четвертая цифры различны, и обе не равны нулю. Докажите, что переставив цифры в этом числе, можно получить другое шестизначное число, также делящееся на 37.

8.2.
Все целые числа от 1 до 2n (n -- некоторое натуральное число) выписали в строчку в некотором порядке, а затем к каждому числу прибавили номер того места, на котором оно стоит. Докажите, что среди полученных сумм найдутся хотя бы две, дающие при делении на 2n одинаковый остаток.

8.3.
Докажите, что для любых положительных чисел x и y справедливо неравенство:

 x³ + y³ x³y⁴ + x⁴y³ .

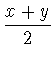
8.4.
На сторонах AB, BC и CA равностороннего треугольника ABC соответственно взяты точки K, M и P так, что AK = BM = CP. Докажите, что точки пересечения прямых AM, BP и CK являются вершинами равностороннего треугольника.

9.1.
Решите в натуральных числах уравнение:

9.2.
В клетки прямоугольной таблицы вписаны числа так, что произведение суммы чисел в любом столбце на сумму чисел в любой строке равняется числу, записанному на пересечении этих столбца и строки. Докажите, что либо сумма всех чисел таблицы равна 1, либо все числа равны нулю.

9.3.
Коэффициенты a, b и c уравнения x³ + ax² + bx + c = 0 по модулю не превосходят 1999. Может ли это уравнение иметь корень, больший, чем 2000?

9.4.
Докажите, что в остроугольном треугольнике точка пересечения высот лежит ближе к наименьшей стороне.

10.1.
Решите в целых числах уравнение:

10.2.
Дан биллиард прямоугольной формы. В его углах имеются лузы, попав в которые шарик останавливается. Шарик выпускают из одного угла биллиарда под углом 45^o к стороне. В какой-то момент он попал в середину некоторой стороны. Докажите, что в середине противоположной стороны шарик побывать не мог.

10.3.
Изобразите на плоскости XOY множество точек, координаты которых удовлетворяют уравнению min (x, y²) = 2.

10.4.
Докажите, что если в треугольнике длина некоторой стороны не превосходит полусуммы двух других сторон, то противолежащий ей угол не превосходит полусуммы двух других углов.

11.1.
Пятьдесят гангстеров стреляют одновременно. Каждый стреляет в ближайшего к себе (а если таковых несколько, то в любого из них), и убивает его наповал. Какое наибольшее число гангстеров может остаться в живых?

11.2.
Придумайте натуральное число, которое после возведения в квадрат начинается с 99 девяток.

11.3.
Без использования калькулятора и другой вычислительной техники докажите неравенство:

2500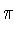 - 100 < 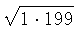+ + 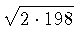... + 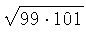< 2500.

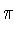11.4.
Пять отрезков таковы, что из любых трех из них можно составить треугольник. Докажите, что из них можно выбрать 3 таких, что треугольник, составленный из них будет остроугольным.