Микроорганизмы

(Автор - А.Р. Данилин, Институт математики и механики УрО РАН)

Микроорганизм МО-2002 прекращает свое существование в конце пятого часа после возникновения. При этом в конце второго часа он производит три подобных себе микроорганизма, а в конце третьего - еще два.

1. В начале эксперимента в колонии микроорганизмов МО-2002 было три новорожденных микроорганизма с одинаковым моментом рождения. Какова будет численность колонии к началу n-го часа эксперимента, если
а) n=5; б) n=7; в) n=11.

(Выписать на бумаге или на экране компьютера соответствующий ответ. При выводе на компьютер сообщить имя соответствующего файла).

2. Описать математическую модель решения задачи и написать программу, определяющую по начальному количеству новорожденных организмов с одинаковым моментом рождения и числу n (входная информация) численность колонии к началу n-го часа эксперимента (выходная информация).

(Автор - А.Р. Данилин, Институт математики и механики УрО РАН)

В некоторых местах водной глади одновременно пролили краску различных цветов, которая стала распространяться по воде, закрашивая ее, с одинаковыми постоянными скоростями. В точках встречи волн дальнейшее распространение их прекращается.

1. Найти формы цветовых пятен, получающихся в результате этого процесса распространения цветовых волн в возможных направлениях после длительного времени и описать границы этих пятен, если
а) n=2;
б) n=3 и источники волн лежат в вершинах треугольника;
в) n=4 и источники волн лежат в вершинах выпуклого четырехугольника с координатами (3;1), (9;3), (3;9), (1;5);
г) и источники волн лежат в точках с координатами (1;1), (13;4), (4;7), (7;4).

(Выписать на бумаге или на экране компьютера соответствующий ответ. При выводе на компьютер сообщить имя соответствующего файла).

2. Написать программу, определяющую по числу красок, координатам центров волн каждого цвета и координатам заданной точки (входная информация) цвет этой точки (выходная информация).

(Автор - академик РАН Н.Н. Красовский, Институт математики и механики УрО РАН)

В один и тот же день первая старушка выезжает из пункта A в пункт B, вторая старушка выезжает ей навстречу из пункта В в пункт А. Каждая старушка выезжает в момент восхода солнца и движется с постоянной скоростью. Старушки встречаются в пункте C в c часов местного времени этого дня и незамедлительно продолжают свое движение. В тот же день первая старушка прибывает в пункт В в b часов местного времени, вторая старушка прибывает в пункт А в a часов местного времени.

Рассмотрим описанную ситуацию в схеме мироздания Птолемея. Согласно этой модели вокруг неподвижной Земли движется Солнце по круговой орбите очень большого радиуса и с центром в центре Земли. При этом Солнце движется равномерно и обходит полную окружность - 360⁰ - за 24 часа абсолютного времени (например, абсолютным можно считать время, показываемое часами, которые везет первая старушка, разумеется, при условии, что она их не переводит). Ограничимся случаем, когда путь АВ проходит по дороге - дуге окружности на поверхности Земли. Причем эта окружность лежит в той же плоскости, что и орбита Солнца. Так как Солнце очень далеко от Земли, то все лучи, приходящие от него в некоторый фиксированный момент абсолютного времени, полагаем параллельными. Солнце движется по своей орбите вокруг Земли в направлении против часовой стрелки. Первая старушка едет в том же направлении. Местное время восхода солнца одинаково в каждом месте на поверхности Земли.

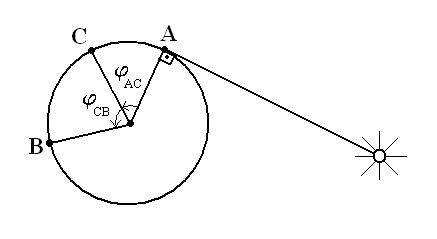
На рисунке изображен момент восхода солнца в пункте A

Угловым перемещением той или иной старушки, которое соответствует перемещению из одной точки в другую по дуге окружности на поверхности Земли, будем называть угол, имеющий вершину в центре Земли и стороны, проходящие через названные точки.

Угловой скоростью назовем угловое перемещение за единицу абсолютного времени.

Пусть
w₁, w₂ - угловые скорости движения первой и второй старушек соответственно;
, - угловые перемещения из пункта A в пункт C и из C в B;

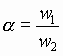
Требуется:
1. по a, b, c и найти время восхода солнца и w₁ , w₂ , , ;
2. проанализировать влияние изменения параметра на решение;
3. промоделировав на компьютере кинематику Солнца и старушек, изобразить соответствующие движения.