Задачи олимпиады

There are several ways to encode an image. In this problem we will consider two representations of an image. We assume that the image consists of black and white pixels. There is at least one black pixel and all black pixels are connected with their sides. Coordinates of black pixels are not less then 1 and not greater then 10. An example of such an image is at the figure.

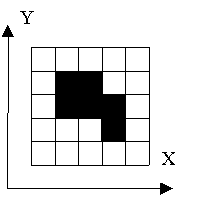
Both representations describe arrangement of black pixels only.

At the first representation we specify number of black pixels in the first line and coordinates of each black pixel in the following lines. Pixels are listed in order of increasing X. In case of equality of X they are listed in order of increasing Y. Image at the figure is encoded as follows:

At the second representation we specify coordinates of the lowest left black pixel in the first line. Each of the following lines contains a description of neighbors for one of the pixels. At first, neighbors of the lowest left pixel are specified, than neighbors of its first neighbor (if it exists) are specified, than neighbors of its second neighbor (if it also exists) follow. When all its neighbors are described the description of the neighbors of its first neighbor follows. The description of the neighbors of its second neighbor follows than and so on.

Each descriptive line contains at most one letter for each neighbor: R for the right, T for the top, L for the left, B for the bottom. If the neighbor was already specified it is not included into the descriptive line and vice-versa. Also there is only one descriptive line for each pixel. Neighbors are listed counter-clockwise starting with the right. Each descriptive line ends with “,”. Last line ends with “.” instead of “,”. Image at the figure is encoded as follows:

There are no leading or tailing spaces in any representation. There is exactly one space between X and Y coordinates.

One representation of the image will be given to your program in the input file. Your program has to write other representation of the image into the output file.

There is a discrete function. It is specified for integer arguments from 1 to N (2<=N<=100000). Each value of the function is longint (signed long in C++). You have to find such two points of the function for which all points between them are below than straight line connecting them and inclination of this straight line is the largest.

There is an N in the first line. Than N lines follow with the values of the function for the arguments 1, 2, …, N respectively.

A pair of integers, which are abscissas of the desired points, should be written into one line of output file. The first number must be less then the second one. If it is any ambiguity your program should write the pair with the smallest first number.

3

2

6

4

1 2

Необходимо посчитать количество “счастливых” билетов с заданной суммой цифр, среди тех, номер которых состоит из 2*N разрядов. “Счастливым” является билет, у которого сумма первых N цифр равна сумме N последних цифр.

Во входном файле находятся два числа разделенных пробелом: первое – N (1<=N<=50); второе – сумма цифр интересующих нас билетов (неотрицательное число не превосходящее 1000).

В качестве ответа необходимо вывести найденное число “счастливых” билетов.

2 2

4

(Условию удовлетворяют билеты: 0101, 0110, 1001, 1010)

В первой строке входного файла записана дата в формате “DD месяц YYYY”, где год вводится из диапазона 1901..2099. Вторая строка содержит целое неотрицательное число - количество дней до интересующей даты, но не более чем до 31-ого декабря текущего (введенного в первой строке) года.

50

Как известно, у многих компьютеров возникли проблемы при наступлении 2000 года. Это связано с тем, что они используют только две цифры для представления года. Поэтому после 1999 года внезапно "наступил" 1900 год. Cледует отметить, что имеется также много других подобных проблем. В некоторых системах для представления времени применяется 32-разрядное целое число. Оно используется, чтобы хранить количество секунд, прошедших c некоторой установленной даты. Таким образом, когда пройдут 2³² секунд (приблизительно 136 лет), год вернется назад к дате, с которой начался отсчет.

Каким образом мы можем разобраться со всем этим беспорядком? Представим, что у нас есть два компьютера C₁ и C₂ с двумя различными ошибками: Один с обычной проблемой Y2K (то есть переходящий к a₁ = 1900 вместо b₁ = 2000) и второй компьютер с переходом к a₂ = 1904 вместо b₂ = 2040. Пусть в какой-то момент времени C₁ показывает год y₁ = 1941 и C₂ - год y₂ = 2005. Мы можем сделать вывод, что реальный год не может быть 1941, т.к. тогда оба компьютера показывали бы правильную дату (1941 год). Если бы был 2005 год, первый компьютер показал бы 1905, поэтому такой вариант также невозможен. Т.к. C₁ показывает 1941, то можно определить, что реальный год - один из следующих: 1941, 2041, 2141 и т.д. Теперь можно вычислить показания C₂ в эти годы: 1941, 1905, 2005 и т.д. Возможно, что настоящим годом является 2141 год.

Итак, ваша задача заключается в том, чтобы написать программу, которая производит эти вычисления. Программа должна находить первое возможное реальное значение года, зная, что показывают компьютеры (y_i) и зная их ошибки (переход к a_i вместо b_i). Обратите внимание, что значение года a_i не может быть больше года создания компьютера. Таким образом, реальный год не может быть меньше любого a_i.

Входной файл содержит несколько наборов данных, для каждого из которых должен быть рассчитан фактический год. Описание варианта начинается со строки, содержащей число компьютеров n (1£ n£ 20). В каждой из следующих n строк содержатся три целых числа y_i, a_i, b_i для каждого компьютера (0£ a_i£ y_i< b_i< 10000). Y_i - год, показываемый компьютером, b_i - год, в котором происходит ошибка (то есть первый год, который не может быть правильно показан этим компьютером) и a_i - год, который компьютер показывает вместо b_i.

Входной файл заканчивается случаем с n=0. Этот случай не должен обрабатываться.

Для каждого набора входных данных выводится строка "The actual year is X." , где X - минимально возможный год, удовлетворяющий условиям. Если не имеется такого года, меньшего чем 10000, выводится строка "Unknown bugs detected.”.

3
1941 1900 2000
2005 1904 2040
1906 1901 1948
2
1992 1900 2000
1904 1900 2000
0

The actual year is 2141.
Unknown bugs detected.

Сеть состоит из нескольких почтовых серверов и абонентов подсоединенных к ним. Всякий абонент подсоединен ровно к одному серверу. Сервера могут быть соединены друг с другом различными способами. Каждый абонент и сервер имеет свой уникальный адрес. Адрес это число . Если абонент этой сети посылает сообщение другому абоненту, то он сначала пересылает это сообщение своему почтовому серверу. Далее почтовый сервер на основании информации, которой он располагает, пересылает это сообщение другому серверу, который в свою очередь может переслать его следующему и так далее, пока сообщение не достигнет сервера, среди абонентов которого встретиться адресат, которому предназначалось письмо. Информация, на основании которой сервер принимает решение о пересылке того или иного сообщения другому серверу храниться в таблице переадресации. Таблица переадресации состоит из нескольких строк, одинакового вида. Стока состоит из нескольких не отрицательных чисел: A, M, D, W, N.

• A – адрес это число
• M – маска адреса это число, которое в двоичном виде можно представить в следующем виде
  
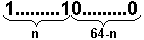
  n – величина маски.
• D – достоверность маршрута: число Î [1; 65535]
• W – цена маршрута Î [1; 65535]
• N – адрес почтового сервера, через который сообщение может быть доставлено

Итак, каждая строчка определяет некоторое множество адресов следующим образом: адрес “B” принадлежит множеству, задаваемому А и М ó (1), где - операция побитового И.

В таблице не может быть двух строк отличающихся только числом N.

Фактически, работа сервера по обработке сообщений сводится к исполнению следующего алгоритма:

Алгоритм переадресации сообщения с адресом “B”:

1. Находятся все записи в таблице переадресации, которые отвечают критерию (1).
2. Среди них выбираются записи с максимальной величиной маски.
3. Среди оставшихся после предыдущего шага записей выбираются записи с максимальным D (степенью доверия).
4. Среди оставшихся после предыдущего шага записей выбираются записи с минимальным W (ценой маршрута).
5. По условию составления таблиц после 4 шага должно остаться не более одной записи. Если записей не осталось вообще, то адресат не доступен. Если же осталась запись без N, то абонент подключен непосредственно к этому серверу, иначе сообщение пересылается на сервер с адресом N.

Программа должна считывать файл input.txt, состоящий из двух частей. Первая содержит таблицу маршрутизации, а вторая адреса, по которым посылаются сообщения. Программа должна обработать эти адреса в соответствии с приведенным выше алгоритмом и таблицей переадресации из этого файла. В выходном файле необходимо для каждого адреса из второй части файла input.txt вывести: или адрес сервера которому в соответствии с таблицей необходимо переадресовать сообщение, или слово “Delivered” в случае если абонент подключен непосредственно к этому серверу, или фразу “Destination unreachable”, во всех остальных случаях.

Входные данные:

Первая строка в файле – число m количество строк в таблице переадресации. mÎ [0; 1000].

Далее идут m строк

Далее до конца файла по одному в каждой строке содержаться адреса для обработки. Их не более 10000.

Выходные данные:

Для каждого адреса вывести или адрес сервера для переадресации или “Delivered”, или “Destination unreachable” в отдельной строке.

Пример: