||🏠
||Чемпионат Урала
||Четвертьфинал ICPC
||УрКОП
||Все соревнования
||Фото
||История
||Новичкам ||
Задачи олимпиады
Задача A. Время собирать камни.
|
Ввод |
INPUT.TXT |
|
Вывод |
OUTPUT.TXT |
|
Лимит времени |
5 сек |
Два игрока играют в следующую игру:
Имеется две кучи из M и N камней соответственно. Игроки ходят по очереди. На каждом ходу из большей кучи камней берется некоторое число камней, кратное их числу в меньшей куче. Выигрывает тот из игроков, кто возьмет последний камень в одной из куч. Очевидно, игра завершается выигрышем одного из игроков.
Требуется написать программу, определяющую по данным M и N, сможет ли первый игрок выиграть при любых действиях второго.
Ввод
Программа должна читать входные данные из файла INPUT.TXT, содержащего два целых положительных числа (M и N) не превосходящих 231 - 1.
Вывод
Программа должна записать в файл OUTPUT.TXT строку "yes", если первый игрок сможет выиграть при любых действиях второго и “no”, если второй игрок может играть так, чтобы не дать выиграть первому.
Пример
INPUT.TXT:
5 7
OUTPUT.TXT:
no
Задача B. Минимальная проекция.
|
Ввод |
INPUT.TXT |
|
Вывод |
OUTPUT.TXT |
|
Лимит времени |
5 сек |
На плоскости xOy координатами вершин задан выпуклый многоугольник. Определить величину его минимальной параллельной проекции на прямую из этой же плоскости.
Ввод
Программа должна читать данные из файла INPUT.TXT, содержащего
- в первой строке – число вершин многоугольника N (2 < N < 100);
- в следующих N строках – по два вещественных числа – координаты x и y вершин (0 <= x, y < = 1000).
Вывод
Программа должна вывести в файл OUTPUT.TXT величину минимальной параллельной проекции многоугольника на прямую, вычисленную с точностью до 3-го знака после десятичной точки.
Пример
INPUT.TXT:
3
0 0
0 10
3 5
OUTPUT.TXT:
3.000
Задача C. Сеть.
|
Ввод |
INPUT.TXT |
|
Вывод |
OUTPUT.TXT |
|
Лимит времени |
5 сек |
Имеется сеть передачи данных, состоящая из нескольких маршрутизаторов, связанных двунаправлненными каналами передачи данных. Каждый из каналов этой сети характеризуется двумя величинами:
- Пропускной способностью n (Мбит/сек)
- Загруженностью k (Мбит/сек)
Загруженность канала не превосходит его пропускной способности.
В некоторый момент времени один из каналов этой сети становится недоступным. В такой ситуации необходимо узнать, можно ли перераспределить (направить данные “в обход”, через другие маршрутизаторы) поток данных этого канала по другим каналам сети так, чтобы для каждого из них выполнялось условие k < = n.
Напишите программу, определяющую это.
Ввод
Программа должна читать данные из файла INPUT.TXT, содержащего:
- в первой строке – число каналов N (2 < N < 1000);
- в следующих N строках – по четыре целых числа a, b, n, k, где a и b – номера соединенных каналом маршрутизаторов (1< = a, b < = 100, a <> b), n – пропускная способность канала ( 1 <= n <= 100), k – загруженность канала (1 <= k <= n).
- в последней строке – номер канала, ставшего недоступным (каналы нумеруются от 1, в порядке поступления их из входного файла).
Вывод
Программа должна вывести в файл OUTPUT.TXT строку "yes", если поток данных недоступного канала можно распределить по другим каналам сети и "no", если этого сделать нельзя.
Пример
INPUT.TXT:
5
1 2 3 1
2 4 2 1
1 4 3 3
1 3 4 2
3 4 5 1
3
OUTPUT.TXT:
yes
Задача D. Самолет
|
Ввод |
INPUT.TXT |
|
Вывод |
OUTPUT.TXT |
|
Лимит времени |
5 сек |
Самолет имеет постоянную (по абсолютной величине) скорость и минимальный радиус разворота R. По заданной начальной позиции самолета (x, y) и вектору его скорости (vx, vy) определите минимальное время, необходимое ему для попадания в точку (0, 0). Под попаданием в точку мы подразумеваем попадание в круг радиуса 0.0001 с центром в этой точке.
Ввод
Программа должна читать данные из файла INPUT.TXT, содержащего пять вещественных чисел R, x, y, vx, vy, где R – минимальный радиус разворота самолета (1 <= R <= 100 ед. длины), x, y – его начальное положение (0 <= x, y <= 1000 ед. длины), vx, vy – компоненты вектора его начальной скорости (1 <= vx, vy <= 100 ед. длины/ед. времени).
Вывод
Программа должна вывести в файл OUTPUT.TXT минимальное число ед. времени, необходимое самолету для достижения точки (0, 0), вычисленное с точностью до 3 знаков после деcятичной точки.
Пример
INPUT.TXT:
5 10 5 0 -1
OUTPUT.TXT:
12.854
Задача E. OCR
|
Ввод |
INPUT.TXT |
|
Вывод |
OUTPUT.TXT |
|
Лимит времени |
10 сек |
В различных областях человеческой деятельности широко применяются алгоритмы распознавания образов. Одно из наиболее известных применений этих алгоритмов – так называемое OCR (Optical Character Recognition) – распознавание текста. Попробуйте и вы изобрести и реализовать в программе алгоритм распознавания десятичных цифр.
На растре шириной 70 и высотой 20 точек расположены изображения цифр. Помимо цифр растр не содержит изображений каких-либо иных объектов. В дальнейшем растр будет обозначаться строками, состоящими из символов ‘:’ (двоеточие), обозначающих белые точки и ‘#’ (диез), обозначающих черные точки. Например:
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::#########:::::###########:::::#######:::::::::::::::::::::::::::::::
::#########:::::###########::::::::####:::::::::::::::::::::::::::::::
:::::::####:::::###########::::::::####:::::::::::::::::::::::::::::::
::::#######:::::####::::::#::##########:::::::::::::::::::::::::::::::
::::#####:::::::####::::::#::##########:::::::::::::::::::::::::::::::
::::#####:::::::###########::##########:::::::::::::::::::::::::::::::
::::#####:::::::::::::::::#::::::::####:::::::::::::::::::::::::::::::
::::#####:::::::::::::::::#:::::#######:::::::::::::::::::::::::::::::
::::###########:::::::::::::::::#######:::::::::::::::::::::::::::::::
и т. д.
В приведенном примере изображено число 293. Все цифры представляют собой наборы прямоугольников, имеющих только вертикальные и горизонтальные стороны. На растре цифры не сливаются между собой и не находятся друг над другом. Иными словами между соседними цифрами всегда существует по крайней мере одна белая вертикальная линия точек.
|
Цифра 0 представляет собой черный прямоугольник, внутри которого содержится белый прямоугольник B, обозначенный на рисунке символами ‘b’. Прямоугольник B не касается сторон черного прямоугольника. |
::::########:::: ::::########:::: ::::########:::: ::::##bbbbb#:::: ::::##bbbbb#:::: ::::##bbbbb#:::: ::::########:::: |
|
Цифра 1 представляет собой просто черный прямоугольник. |
:::::::::::::::: ::::########:::: ::::########:::: :::::::::::::::: :::::::::::::::: :::::::::::::::: :::::::::::::::: |
|
Цифра 2 представляет собой набор из пяти смежных черных прямоугольников A, B, C, D, E, обозначенных на рисунке символами ‘a’, ‘b’, ‘c’, ‘d’, ‘e’ соответственно. Прямоугольники расположены один под другим, в том порядке, в котором они перечислены. Правые стороны прямоугольников A, B, C лежат на одной прямой, расположенной правее правой стороны прямоугольника D. Левые стороны прямоугольников C, D, E лежат на одной прямой, расположенной левее левой стороны прямоугольника B. Прямоугольник A шире прямоугольника B, прямоугольник E шире прямоугольника D, а прямоугольник C шире B и шире D. |
::::::aaaaaa:::: :::::::::bbb:::: ::::cccccccc:::: ::::cccccccc:::: ::::cccccccc:::: ::::dd:::::::::: ::::eeeeeeeeee:: |
|
Цифра 3 представляет собой набор из пяти смежных черных прямоугольников A, B, C, D, E, обозначенных на рисунке символами ‘a’, ‘b’, ‘c’, ‘d’, ‘e’ соответственно. Прямоугольники расположены один под другим, в том порядке, в котором они перечислены. Правые стороны всех прямоугольников лежат на одной прямой. Прямоугольник A шире прямоугольника B, а прямоугольник C шире прямоугольников B и D, прямоугольник E шире прямоугольника D |
::::::aaaaaa:::: :::::::::bbb:::: ::::cccccccc:::: ::::cccccccc:::: :::::::::::d:::: :::::::::::d:::: :::::::::eee:::: |
|
Цифра 4 представляет собой набор из трех смежных черных прямоугольников A, B, C, обозначенных на рисунке символами ‘a’, ‘b’, ‘c’ соответственно. Прямоугольники расположены один за другим, слева направо, в том порядке, в котором они перечислены. Нижние стороны прямоугольников A и B лежат на одной прямой. Верхние стороны прямоугольников A и C расположены выше верхней стороны прямоугольника B. Нижняя сторона прямоугольника C расположена ниже нижней стороны прямоугольника B. |
::::::::::cc:::: :::aaa::::cc:::: :::aaa::::cc:::: :::aaabbbbcc:::: ::::::::::cc:::: ::::::::::cc:::: ::::::::::cc:::: |
|
Цифра 5 представляет собой набор из пяти смежных черных прямоугольников A, B, C, D, E, обозначенных на рисунке символами ‘a’, ‘b’, ‘c’, ‘d’, ‘e’ соответственно. Прямоугольники расположены один под другим, в том порядке, в котором они перечислены. Левые стороны прямоугольников A, B, C лежат на одной прямой, расположенной левее левой стороны прямоугольника D. Правые стороны прямоугольников C, D, E лежат на одной прямой, расположенной правее правой стороны прямоугольника B. Прямоугольник A шире прямоугольника B, прямоугольник E шире прямоугольника D, а прямоугольник C шире B и шире D. |
::::aaaaa::::::: ::::bbb::::::::: ::::cccccccc:::: ::::cccccccc:::: ::::cccccccc:::: ::::::::::dd:::: ::eeeeeeeeee:::: |
|
Цифра 6 представляет собой два смежных черных прямоугольника A и B, обозначенных на рисунке символами ‘a’ и ‘b’. Прямоугольники A и B расположены один под другим, в том порядке, в котором они перечислены. Левые стороны прямоугольников A и B лежат на одной прямой. Прямоугольник B шире прямоугольника A. Внутри прямоугольника B расположен белый прямоугольник C, обозначенный на рисунке символами ‘c’. Прямоугольник C не касается сторон прямоугольника B. |
::::aaa::::::::: ::::aaa::::::::: ::::aaa::::::::: ::::bbbbbbbb:::: ::::bbbbbbbb:::: ::::bbbcccbb:::: ::::bbbbbbbb:::: |
|
Цифра 7 представляет собой два смежных черных прямоугольника A и B, обозначенных на рисунке символами ‘a’ и ‘b’. Прямоугольники A и B расположены один под другим, в том порядке, в котором они перечислены. Правые стороны прямоугольников A и B лежат на одной прямой. Прямоугольник A шире прямоугольника B. |
::::aaaaaaaaa::: ::::aaaaaaaaa::: ::::aaaaaaaaa::: :::::::::::bb::: :::::::::::bb::: :::::::::::bb::: :::::::::::bb::: |
|
Цифра 8 представляет собой черный прямоугольник, внутри которого расположены не касающиеся друг друга и сторон этого прямоугольника белые прямоугольники A и B. Нижняя сторона прямоугольника A расположена выше верхней стороны прямоугольника B. |
::::#########::: ::::##aaaaa##::: ::::#########::: ::::####bbbb#::: ::::####bbbb#::: ::::####bbbb#::: ::::#########::: |
|
Цифра 9 представляет собой два смежных черных прямоугольника A и B, обозначенных на рисунке символами ‘a’ и ‘b’. Прямоугольники A и B расположены один под другим, в том порядке, в котором они перечислены. Правые стороны прямоугольников A и B лежат на одной прямой. Прямоугольник A шире прямоугольника B. Внутри прямоугольника A расположен белый прямоугольник C, обозначенный на рисунке символами ‘c’. Прямоугольник C не касается сторон прямоугольника A. |
::::aaaaaaaa:::: ::::aaccccaa:::: ::::aaaaaaaa:::: ::::aaaaaaaa:::: :::::::::bbb:::: :::::::::bbb:::: :::::::::bbb:::: |
Ввод
Программа должна читать данные из файла INPUT.TXT, содержащего 20 строк по 70 символов, в указанном выше формате. Строки разделены символами “возврат каретки” и “перевод строки”.
Вывод
Программа должна найти в растре все цифры и вывести их в том порядке (слева направо) в котором они расположены в растре.
Пример
INPUT.TXT
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
:::::::::::::::::::::::::::::::::::::::::;::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
:::::::::::::::::::::::::::::::::::::::::#::#####:######:######:::::::
::::::::::::::::::::::::::::::::::::::::::::#:###:####:#:#:####:::::::
::::::::::::::::::::::::::::::::::::::::::::#####:######:######:::::::
:::::::::::::::::::::::::::::::::::::::::::::####::::###::::::#:::::::
:::::::::::::::::::::::::::::::::::::::::::::::::::::###::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
OUTPUT.TXT
1999
Задача F. Сумма чисел Фибоначчи.
|
Ввод |
INPUT.TXT |
|
Вывод |
OUTPUT.TXT |
|
Лимит времени |
40 сек |
Числа Фибоначчи представляют собой последовательность {an}, где a1=a2=1, " n>2 an=an-1+an-2:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | и т.д. |
|---|---|---|---|---|---|---|---|---|
| an | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
Ввод
Во входном файле INPUT.TXT содержится целое число N (от 0 до 1000), после которого идут ровно N чисел bi (bi от 1 до 2000).
Вывод
Программа должна записать в файл OUTPUT.TXT целое число –
сумму N чисел Фибоначчи, порядковые номера которых перечислены, т.е.
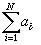
Пример
INPUT>TXT
4
13
1
7
50
OUTPUT.TXT
12586269272
Задача G. Компилятор.
|
Ввод |
INPUT.TXT |
|
Вывод |
OUTPUT.TXT |
|
Лимит времени |
5 сек |
Пусть задан некая программа, описываемая следующей грамматикой:
<программа> ::= "BEGIN" <разделитель> {<оператор>"; "<разделитель>} "END"
<оператор> ::= <условный_оператор> | <безусловный_оператор>
<безусловный_оператор> ::= "PRINT " <формула>{","<формула>}
| <переменная>"="<формула>
<формула> ::= [знак]<операнд> {<знак><операнд>}
<знак> ::= "+" | "-"
<операнд> ::= <переменная> | <число>
<переменная> ::= "A" | "B" | "C" | … | "X" | "Y" | "Z"
<число> ::=<цифра>{цифра}
<цифра> ::= "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9"
<условный_оператор> ::= "IF "<условие> " THEN"<разделитель> <безусловный_оператор>
[“ELSE“ <разделитель><безусловный_оператор>]
<условие> ::= <формула><знак_отношения><формула>
<знак_отношения> ::= ">" | "<" | "=="
<разделитель> ::= <разделительный_символ> {<разделительный_символ>}
<разделительный_символ> ::= " " | ¿
где в кавычках приведены терминальные символы, в { } находится выражение, которое может быть повторено 0 или более раз, в [ ] - выражение, которое может быть повторено 0 или 1 раз; знак | означает альтернативу. Под <разделительный_символ> понимаем следующие символы: пробел и “возврат каретки” с “переводом строки”.
Ваша задача промоделировать работу заданной во входном файле программы, отвечающей заданной грамматике и вывести результаты работы в выходной файл, учитывая следующие условия.
- При выполнении безусловного оператора PRINT вы должны вывести в файл полученные результаты формул – операндов данного оператора, разделяя каждый результат символами перевода строки и возврата коретки.
- При выполнении безусловного оператора "=" происходит присваивание переменной, стоящей справа значение формулы, находящейся слева
- При выполнении условного оператора IF в случае истинности условия программа должна выполнить безусловный оператор, стоящий после ключевого слова THEN; в противном случае – безусловный оператор, стоящий после ключевого слова ELSE в случае его наличия.
- Значения формул и операндов лежат в диапозоне –32768 … 32767
- Программа не содержит каких-либо синтаксических и логических ошибок.
Ввод
Во входном файле INPUT.TXT содержится текст программы, описанной выше грамматикой и удовлетворяющей приведенным выше условиям. Количество строк текста не более 100.
Вывод
Программа должна записать в файл OUTPUT.TXT результаты работы исходной программы.
Пример
|
INPUT.TXT BEGIN A=5; B=8; PRINT A, A, B, A+B+5; END |
OUTPUT.TXT 5 5 8 18 |